Luis Gonzalo Sánchez Giraldo::Research

Overview

Information Theoretic Learning

• This work focuses on studying the properties of certain functionals applied to positive definite matrices that expose similar properties of an entropy functional Ref. By using positive definite kernels, we can estimate quantities with similar properties of entropy functionals directly from data. The proposed estimators of entropy using positive definite kernels bring the representational advantages of kernel methods along with some nice convergence properties; the rate of convergence can be independent of the input space dimensionality. 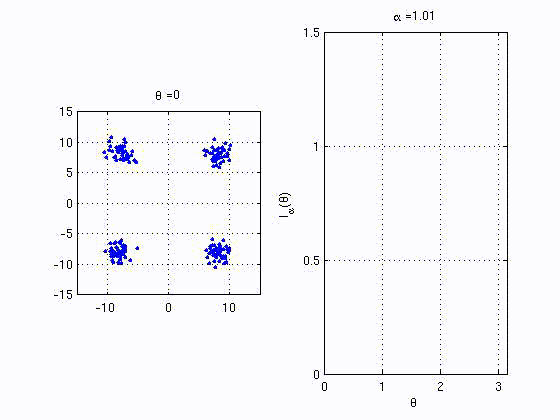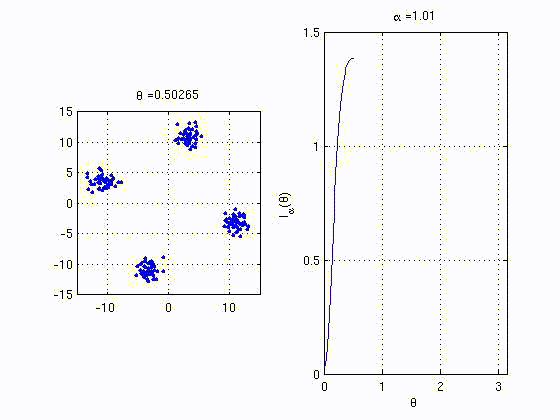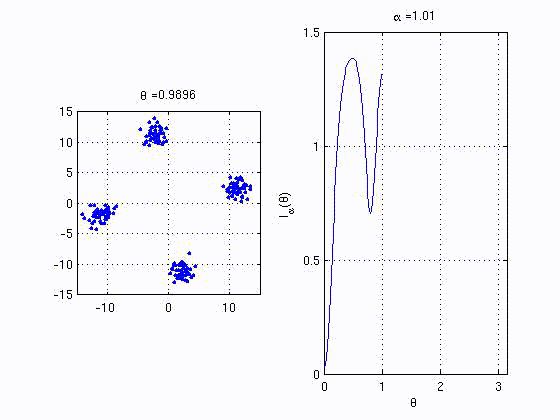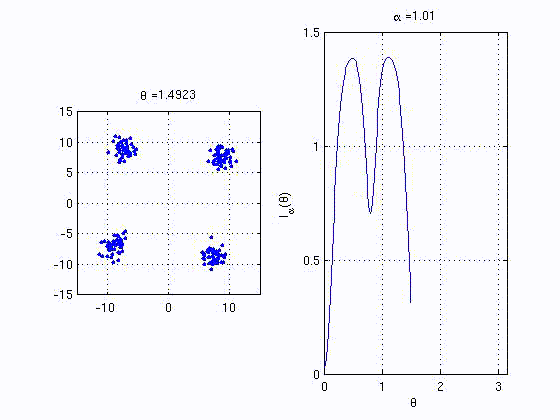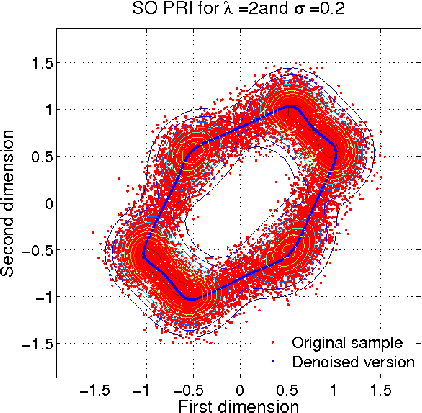For testing independence, our estimators improve upon other estimators such entropic graphs and the recently proposed kernel based statistics. The animation below shows the behaviour of one of the proposed quanties that behaves similar to mutual information. The right plot is the analogue MI between the variables corresponding to the horizontal and vertical axes in the left plot.

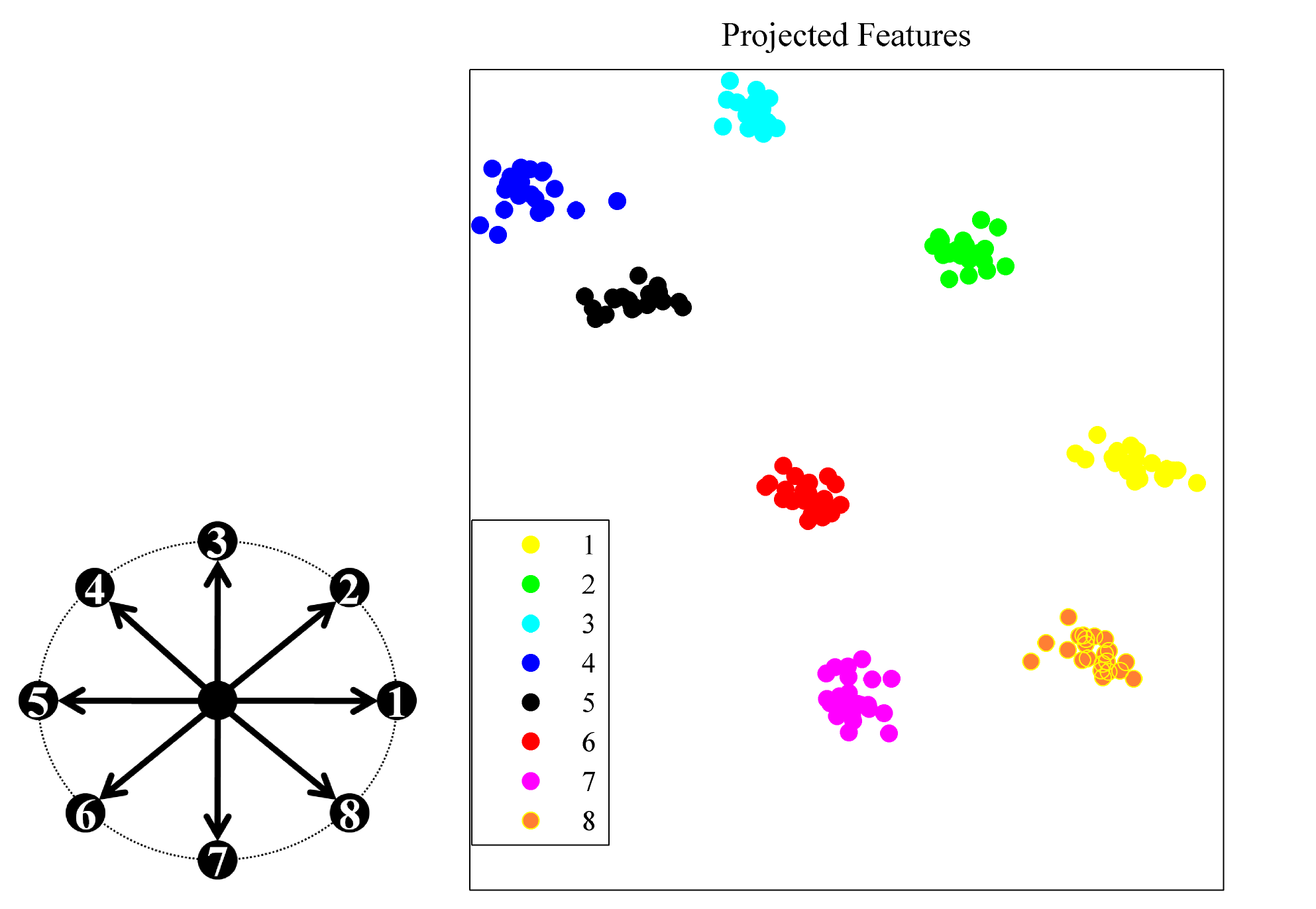
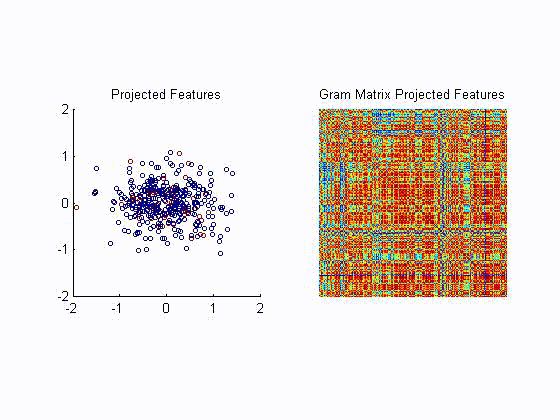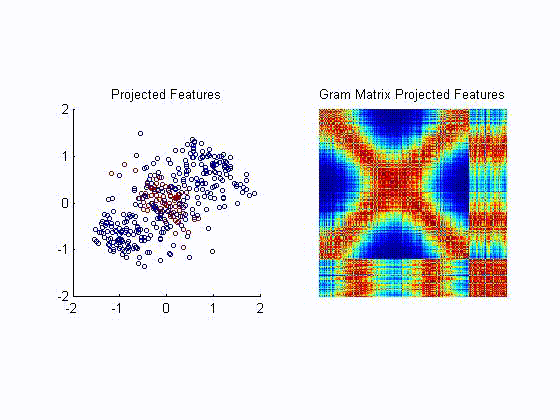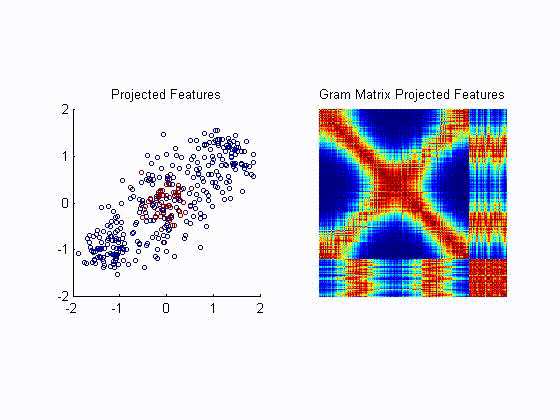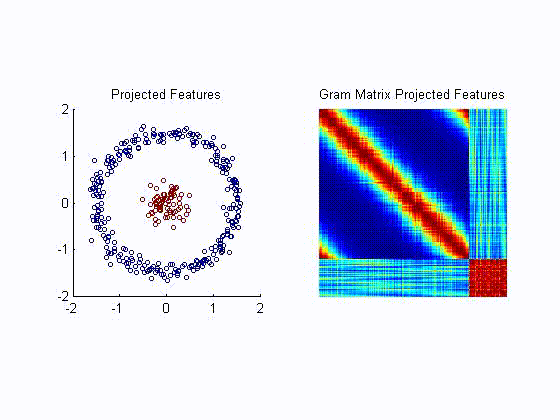
• For metric learning Ref, we propose to minimize a kernel based analogue of conditional entropy between a label variable and a given transformation of the input. The resulting metric is able to preserve the class structure even after drastic reductions in dimensionality and achieving state of the art results. The following example, illustrates the ability of the proposed algortihm to unravel a two dimensional projection of the data that preserves the label information without requiring the samples to be lineraly separable. The left plot is the resulting projection after each training iteration. The right plot is tha resulting Gram matrix that shows how tha algorithm unveils the block struture corresponding to the class information.

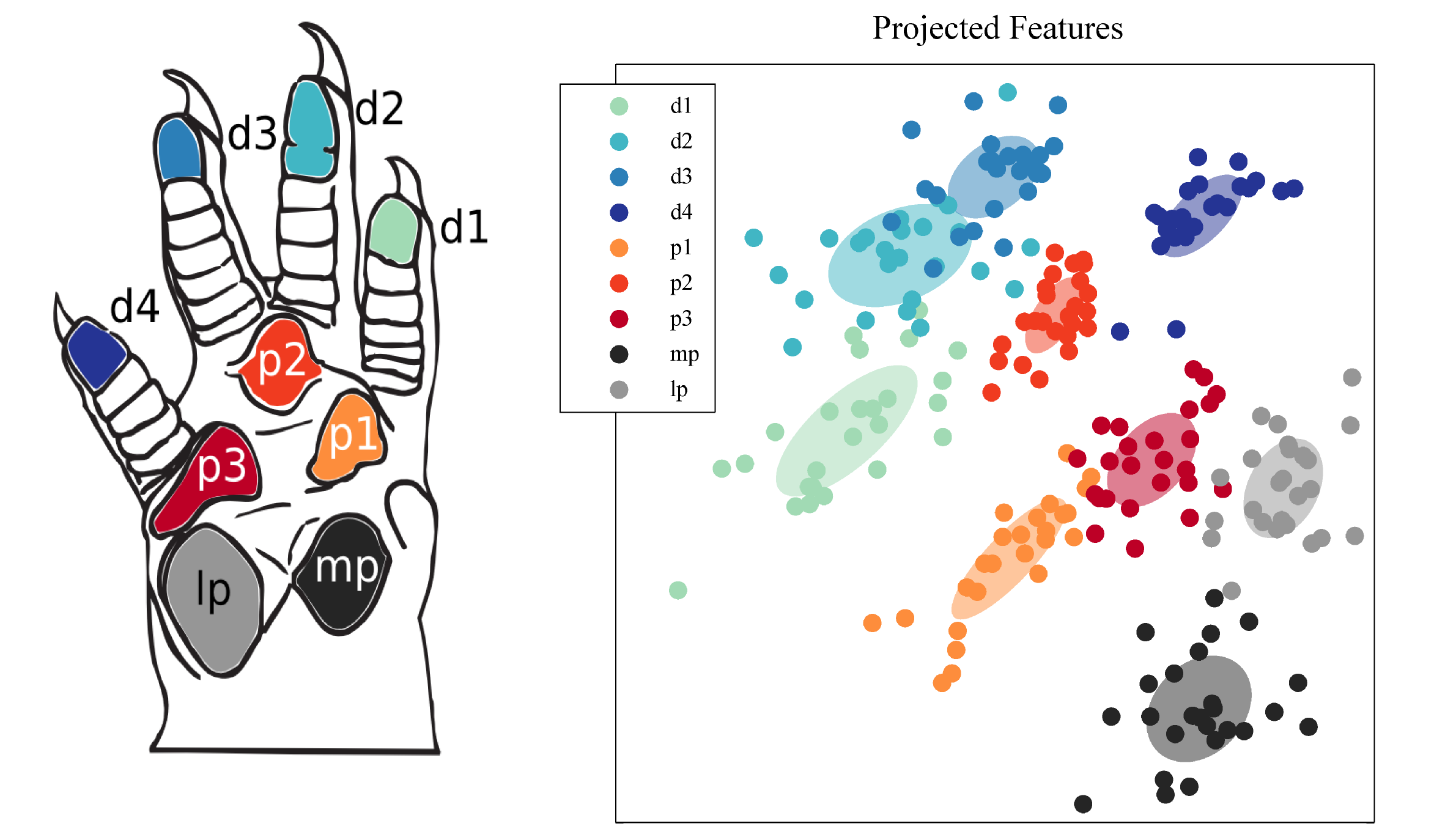
• We have applied our metric learning algorithm to visualization of high-dimensional neural data Ref. Namely, we visualize the motor cortex neuronal firing rates of a macaque during a center-out reaching task, and local field potentials in the somatosensory cortex of a rat during tactile stimulation of the forepaws. The obtained 2 dimensional projections preserve the natural topology of targets in the reaching task, and the peripheral touch sites of the forepaws.

• Renyi's entropy of order 2 can be estimated using Parzen windows. Interestingly, this estimator can be efficiently approximated using a rank deficient decomposition of a Gram matrix. Our work in Ref, utilizes this approximation for unsupervised learning. The algorithm poses the problem of unsupervised learning as a trade off between information preservation and entropy minimization. Furthermore, in Ref we propose a reproducing kernel Hilbert space (RKHS) formulation of this problem. In this case, we obtain an pseudo-convex optimization problem that can be solved with techniques such sequential minimal optimization (initially proposed for support vector machines). The algorithm can be considered a support vector type algorithm in the sense that the solution is expressed with a subset of the initial set of data points Report. This approach compares favourably against other kernel-based feature extractors such as kernel PCA and kernel entropy component analysis, with the advantage of expressing the solution as a reduced data set.

   

• For non-rigid image registration, we proposed information theoretic matching functions that are robust to noise and outliers Ref_A Ref_B. Sets of points are represented by densities and aligned via a non-rigid transformation such that a measure of divergence is minimized. Namely, we use the Cauchy-Schwartz divergence which computes the angle between densities in L₂. The proposed matching algorithm performs well for various degrees of transformation and levels of noise.

Online Kernel-Based Learning

• Along with support vector machines, kernel principal component analysis are among the most representative algorithms that exploit this implicit representation. The kernel principal components are obtained by solving eigenvalue problem involving a matrix of pairwise evaluations of the input data samples called the Gram matrix. In signal processing applications, data often arrives in an online fashion. We proposed an online kernel PCA algorithm using a fixed point update rule based on a Rayleigh quotient in the RKHS Ref. The fixed point update convergences faster than the generalized Hebbian learning algorithm an it does not require setting a step size parameter.

• I have also taken part on the development of a kernel based temporal difference learning algorithm Ref. This method has been applied in reinforcement learning to nonlinear approximations of state-action value functions from which optimal policies can be derived. A practical advantage of our approach is that the relation between step size and eligibility traces is well understood when normalized kernel functions are utilized allowing for stable learning rates to be easily set. Moreover, there is no requirement for parameter initialization and we have empirically observed that it outperforms other conventional non-linear methods that are based on temporal differences. This algorithm has been applied to neural decoding in reinforcement learning-based brain machine interfaces.